使用 ap 實現 S Combinator

Binary Function 若第二個 Argument 須先經過其他 Unary Function 運算再傳入，此為 S Combinator，可使用 ap 實現。

Version

Ramda 0.27.1

let data = 10

let f = x => x + 3 * x

f (data) // ?

若使用 operator，會直接使用 + 與 x。

s000

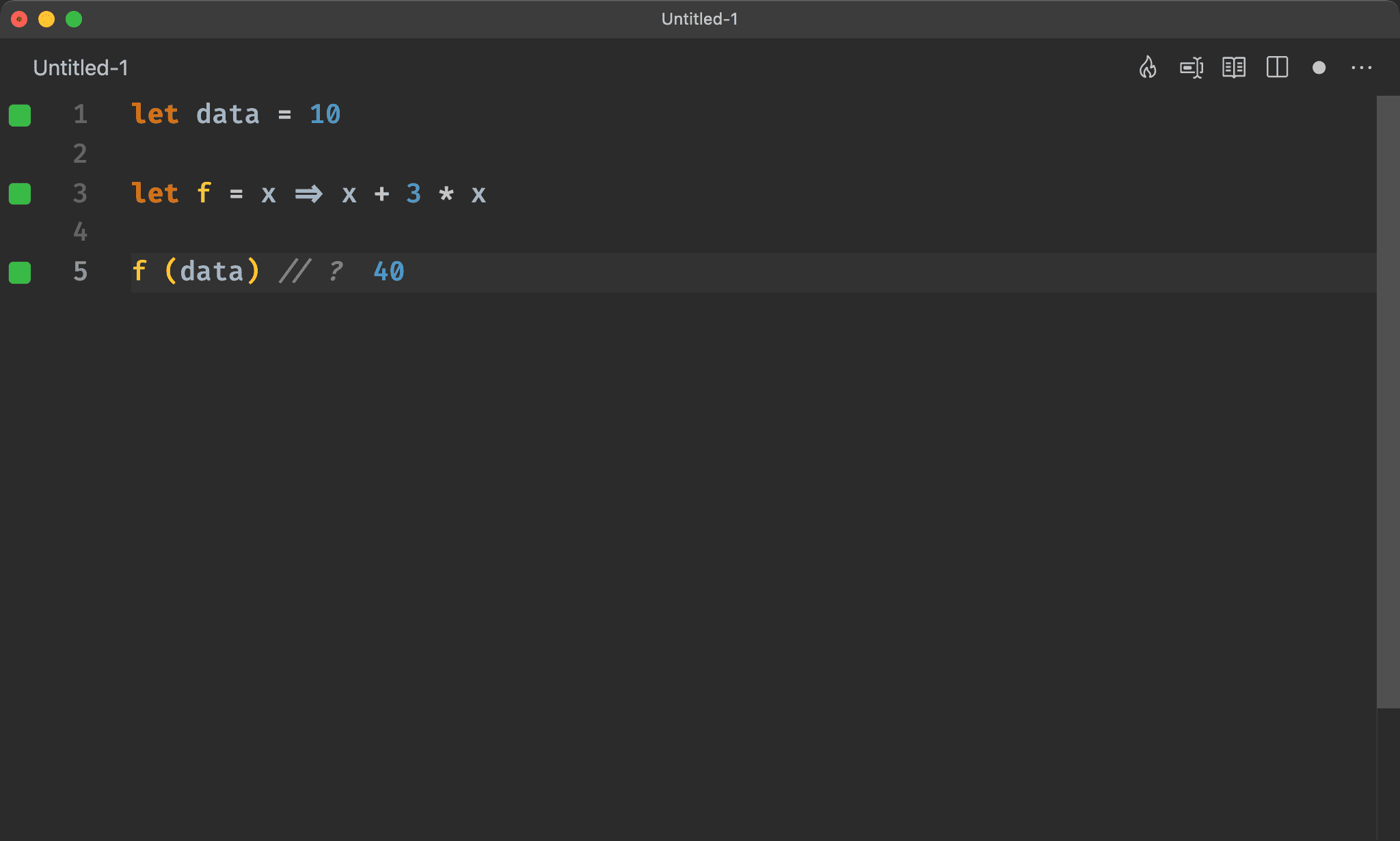
import { add, multiply } from 'ramda'

let data = 10

let f = x => add (x) (multiply (3) (x))

f (data) // ?

若將 operator 改成 function，會發現 add 第二個 argument 須先經過 multiply 運算過才傳入。

s001

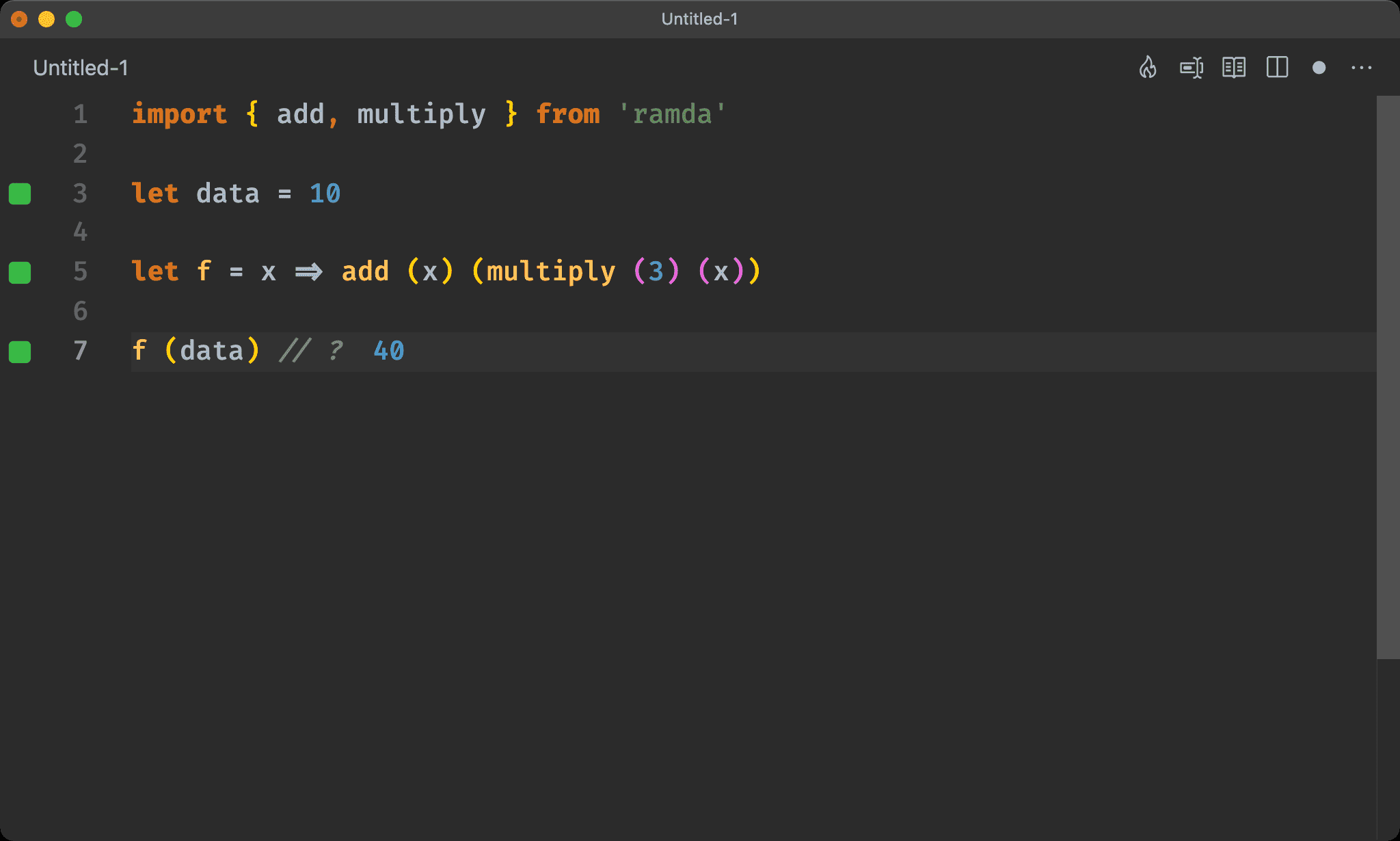
import { add, multiply, converge, identity as I } from 'ramda'

let data = 10

converge (add) ([I, multiply (3)]) (data) // ?

一般為了 Point-free，都會朝向 pipe、compose、useWith 或 converge 這些 function 著手。

因為發現 add 是實質最後一個 function，第一個 argument 不變，第二個 argument 經過 multiplay (3)，很直覺會朝向 converge 重構。

當出現 converge (f) ([I, g]) 時，它等效於 ap (f) (g)

s003

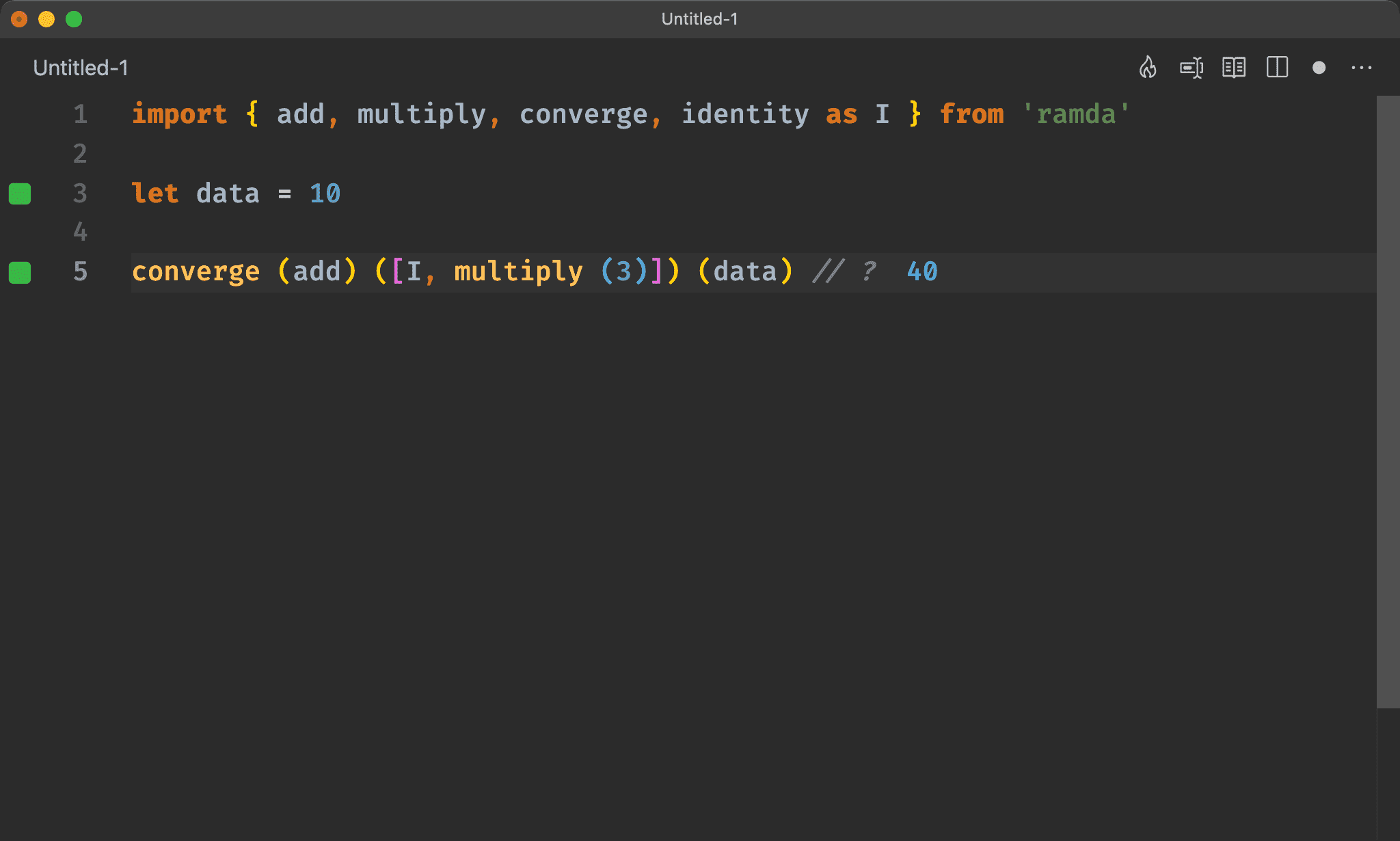
import { ap, add, multiply } from 'ramda'

let data = 10

ap (add) (multiply (3)) (data) // ?

這種第二個 argument 須經過運算後再傳入的 pattern，就是所謂的 S Combinator，其中 S 為 S equence，可使用 ap 組合使其 Point-free。

ap (f) (g) (x) = f (x) (g (x))

而 ap 正是 S Combinator 的實現。

ap
(a → b → c) → (a → b) → a → c
實現 S Combinator

(a → b → c)：傳入 binary function

(a → b)：傳入 unary function

a：為 data

c：回傳結果

ap 原本定義為：

ap
Apply f => f (a -> b) -> f a -> f b
將 function 包進 Apply 再傳入 ap 改變 Apply 內部值

f (a -> b)：傳入包進 Apply 的 function

f a：data 為 Apply

f b：回傳新 Apply

由於 Function 也是 Apply，因此 data 為 unary function，而第一個 argument 相當於 unary function 包進 unary function 傳入，因此為 binary function。

s002

chain (f) (g) (x) = f (g (x)) (x)

眼尖的人應該會發現 ap 與 chain 非常接近：

ap 在第二個 argument 先經過其他 function 運算，而 chain 則在第一個 argument 先經過其他 function 運算。

Binary function 若只有一個 argument 經過 function 運算，可使用 ap 或 chain 組合
Binary function 若兩個 argument 都需經過 function 運算，可使用 converge 組合
若一開始看不出使用 ap，可先重構成 converge，當發現 converge (f) ([I, g]) 時再重構成 ap
ap 之所以能實現 S combinator，因為 unary function 也是 Apply，當 unary function 包進 unary function 時就成為 binary function