點燈坊

失くすものさえない今が強くなるチャンスよ

Monad 並沒有 Composition Law

Sam Xiao's Avatar 2021-07-24

Functor 的 Composition Law 是重構 Functor 常見技巧，但可惜 Monad 並不存在 Composition Law，但仍可使用 Function 都有的 Associativity Law 與 Monad 特有的 Associativity Law 來組合。

Version

Fantasy Land 5.0.0

chain

import { pipe, compose, chain, Just, add } from 'sanctuary'

let data = 1

let f = compose (Just) (add (1))
let g = compose (Just) (add (2))
let h = compose (Just) (add (3))

pipe ([
  f,
  chain (g),
  chain (h)
]) (data) // ?

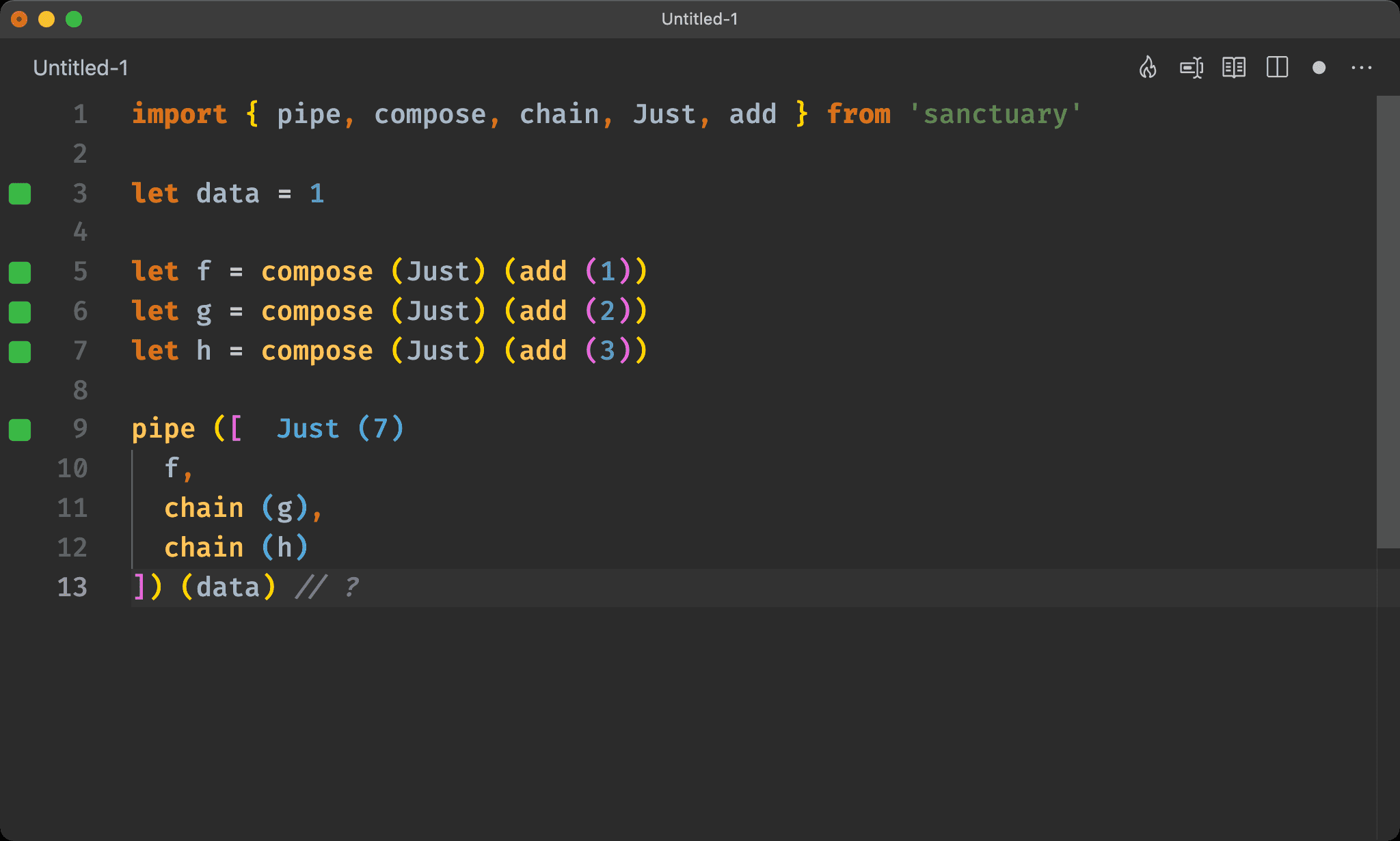
f、g 與 h 都是回傳 Maybe 的 function，若要將依序套用這 3 個 function，可使用 pipe 組合 f、g 與 h。

唯 3 個 funciton 都回傳 Maybe，因此必須使用 chain 將 Maybe 與回傳 Maybe 的 function 綁定。

no000

Composition

import { pipe, compose, chain, Just, add } from 'sanctuary'

let data = 1

let f = compose (Just) (add (1))
let g = compose (Just) (add (2))
let h = compose (Just) (add (3))

let t = pipe ([
  g,
  h
])

pipe ([
  f,
  chain (t)
]) (data) // ?

第 9 行

let t = pipe ([
  g,
  h
])

根據使用 map 的經驗，直覺會想將在 chain 內的 g 與 h 先組合起來。

14 行

pipe ([
  f,
  chain (t)
]) (data) // ?

然後一次傳給 chain，這就是 Functor 的 composition。

Composition Law
fmap f . fmap g = fmap (f . g)
多次 map 相當於先組合 function 再一次傳入 map

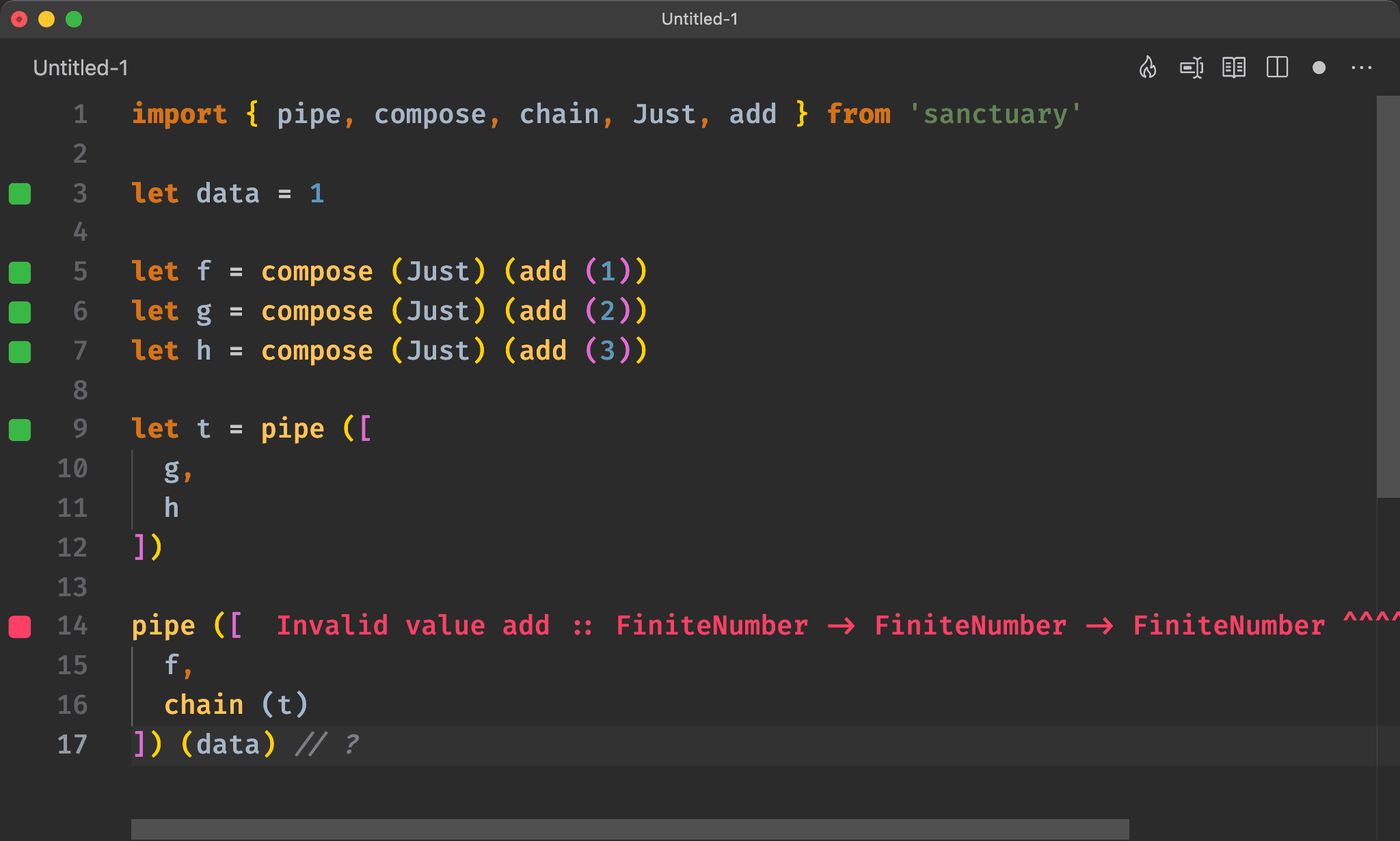
no001

但會發現 Sanctuary 會抱怨 type 不合而無法組合，因為 Monad 並不存在 composition law，因此 chain 無法如 map 那樣組合。

Associativity

import { pipe, compose, chain, Just, add } from 'sanctuary'

let data = 1

let f = compose (Just) (add (1))
let g = compose (Just) (add (2))
let h = compose (Just) (add (3))

let t = pipe ([
  chain (g),
  chain (h)
])

pipe ([
  f,
  t
]) (data) // ?

第 9 行

let t = pipe ([
  chain (g),
  chain (h)
])

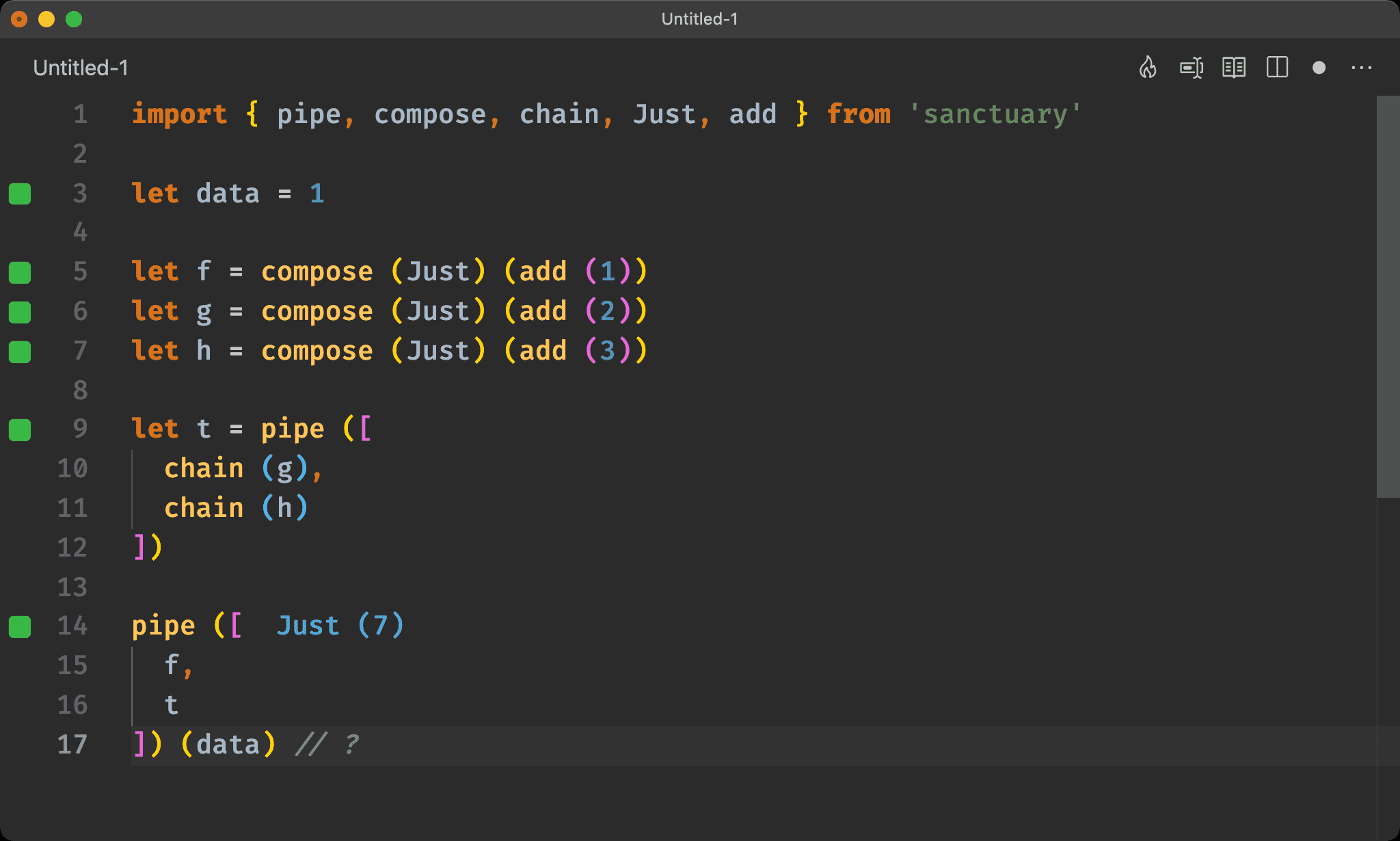
一樣組合 g 與 h，但改用 function 都支援的 associativity law，因此 chain 也要帶進 pipe。

14 行

pipe ([
  f,
  t
]) (data) // ?

如此將 t 一次傳進 pipe 即可。

但可發現 f 明明也是回傳 Maybe 的 function，卻沒有一起組合

no002

import { pipe, compose, chain, Just, add } from 'sanctuary'

let data = 1

let f = compose (Just) (add (1))
let g = compose (Just) (add (2))
let h = compose (Just) (add (3))

let t = pipe ([
  f,
  chain (g),
  chain (h)
])

t (data) // ?

第 9 行

let t = pipe ([
  f,
  chain (g),
  chain (h)
])

也可繼續使用 associativity 將 f 也整進 pipe。

但這樣似乎跟沒 refactoring 一樣，又回到原點

Monad’s Associativity

import { pipe, compose, chain, Just, add } from 'sanctuary'

let data = 1

let f = compose (Just) (add (1))
let g = compose (Just) (add (2))
let h = compose (Just) (add (3))

let t = pipe ([
  chain (f),
  chain (g),
  chain (h)
])

t (Just (data)) // ?

第 9 行

let t = pipe ([
  chain (f),
  chain (g),
  chain (h)
])

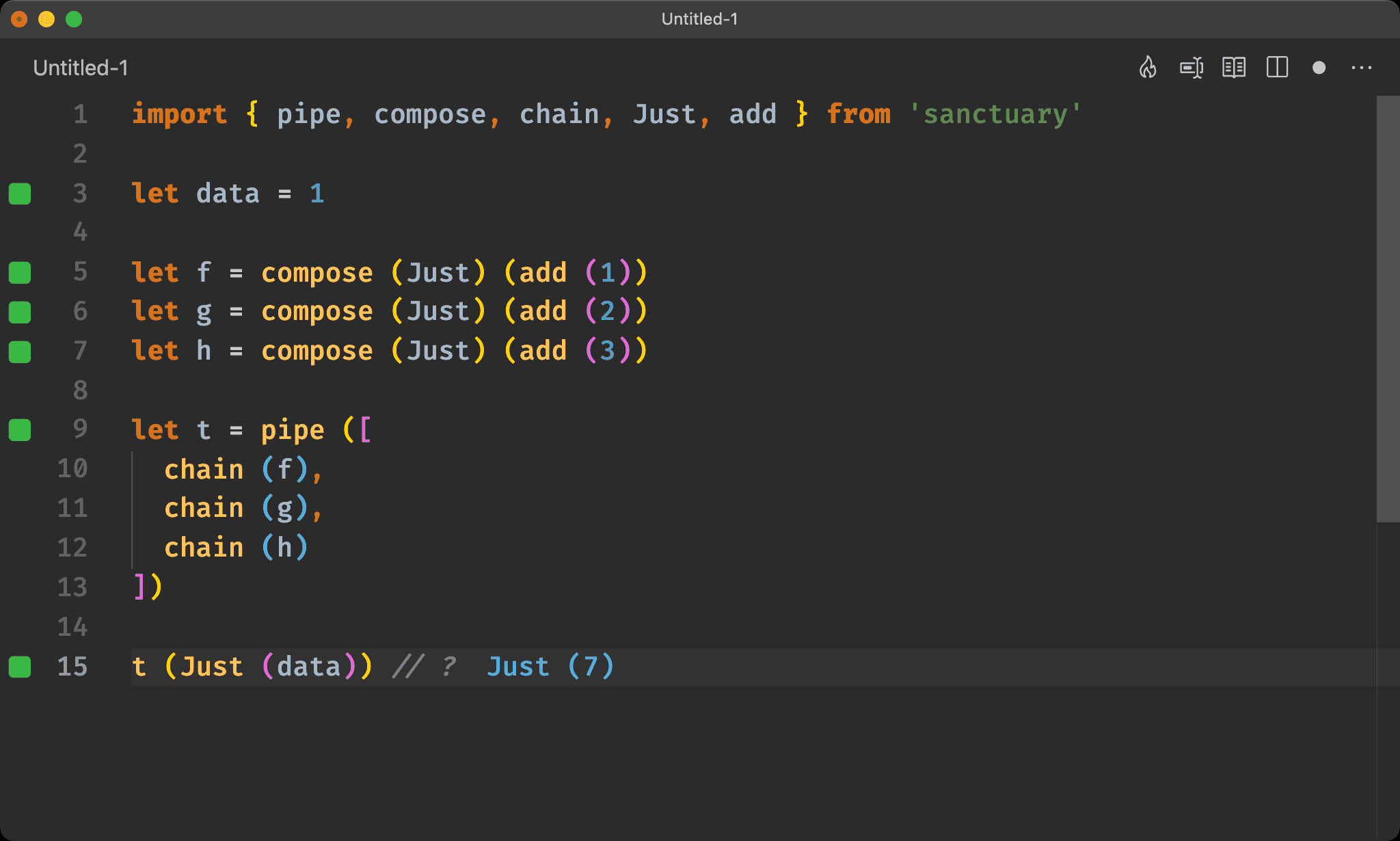
由於 Maybe 也是 Monad，因此也可使用 Monad 的 associativity law 來組合 f、g 與 h。

Associativity
(m >>= f) >>= g === m >>= (\x -> f x >>= g)
先將 value 包進 Monad 再連續使用 chain 與 function 綁定，與 value 先經過 function 運算最後包進 Monad 結果相同

15 行

t (Just (data)) // ?

唯 data 必須先包進 Maybe 內。

no003

Conclusion

  • 不見得只能使用 composition 組合 function，事實上 associativity 也能組合 function
  • Monad 並不存在 Functor 那樣的 composition law，但仍可用 function 共通的 associatively law 或 Monad 的 associativity law 來組合

# Category