點燈坊

失くすものさえない今が強くなるチャンスよ

深入淺出 Monad Laws

Sam Xiao's Avatar 2021-07-24

Monad 遵循 3 個 Monad Laws，專門描述 chain 的 3 個特性，包含兩個 Identity Law 與一個 Associativity Law。

Version

Fantasy Land 5.0.0

Left Identity

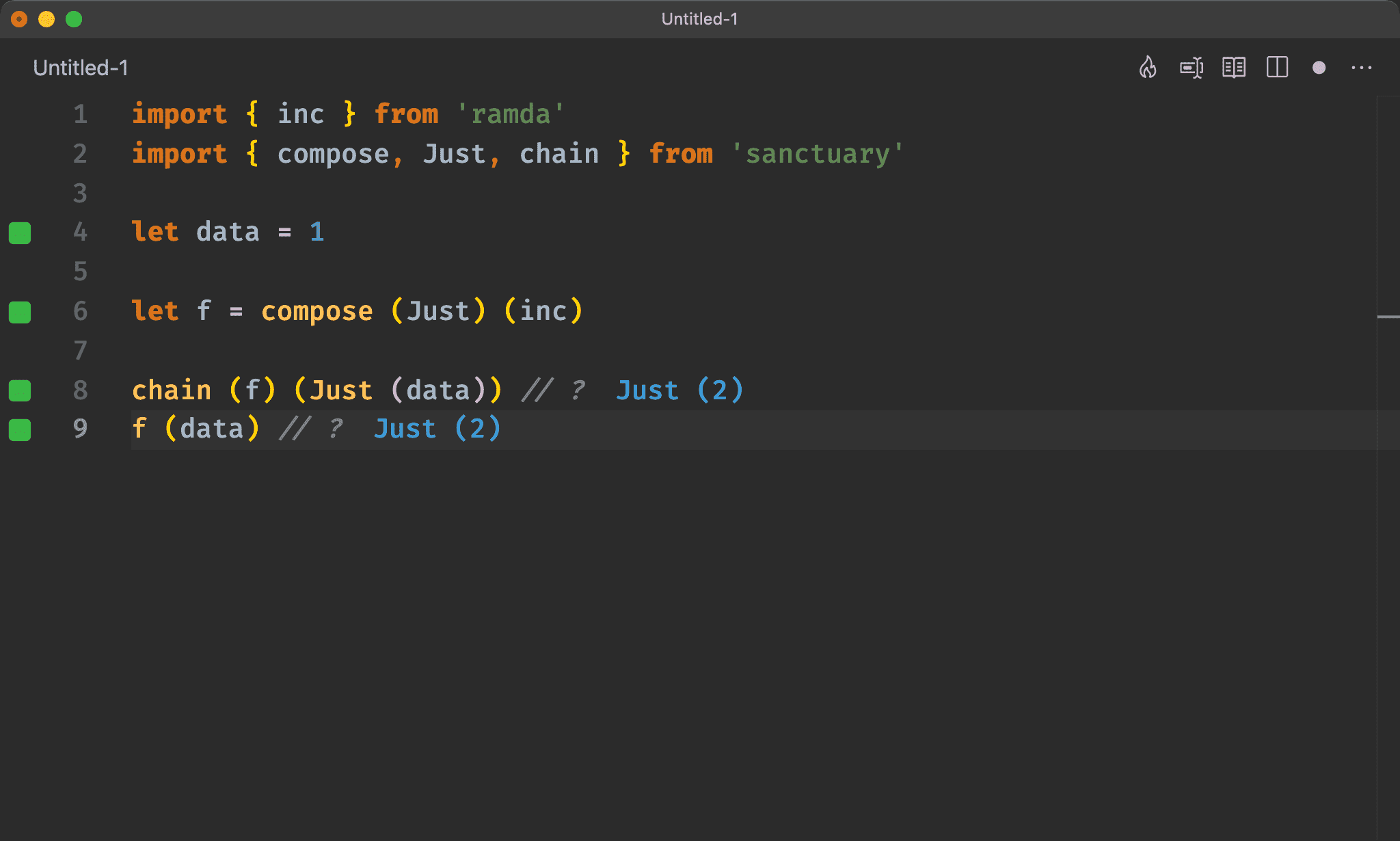
import { inc } from 'ramda'
import { compose, Just, chain } from 'sanctuary'

let data = 1

let f = compose (Just) (inc)

chain (f) (Just (data)) // ?
f (data) // ?
  • 使用 chain 將 Monad 與回傳 Monad 的 function 綁定
  • 直接將 value 傳入回傳 Monad 的 function

兩者結果相同。

也就是 chain 能將 Moand 與回傳 Monad 的 function 綁定並回傳新 Monad，看似改變 Monad 內部 value。

這也是 chain 最基本功能。

Left Identity
return a >>= f === f a

  • return a >>= f：使用 chain 將 Monad 與 function 綁定
  • f a：value 直接傳入 function
  • ===：兩者結果相同

因為 return 在 >== 左側，故稱 Left Identity

laws000

Right Identity

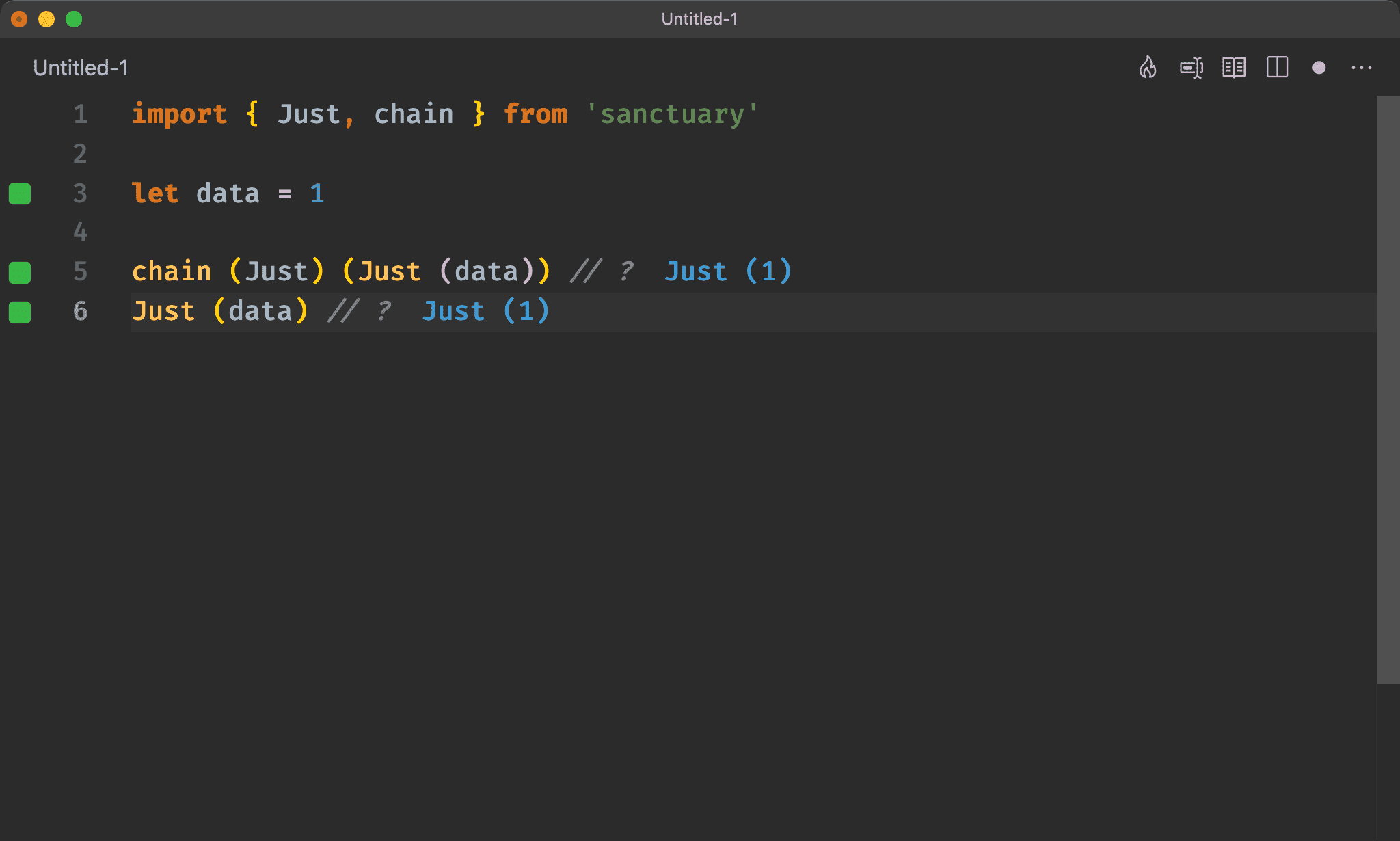
import { Just, chain } from 'sanctuary'

let data = 1

chain (Just) (Just (data)) // ?
Just (data) // ?
  • 使用 chain 將 Monad 與 Just 綁定
  • 將 value 直接包進 Monad

兩者結果相同。

也就是使用 chain 將 Monad 與 Just 綁定時不會改變 Monad。

Just 相當於 chain 的 identity，當發現 chain (Just) 時，可直接消去不影響結果。

Right Identity
m >>= return === m

  • m >>= return：使用 chain 將 Monad 與 return 綁定，return 就是 Just
  • m：Monad
  • ===：兩者結果相同

因為 return 在 >== 右側，故稱 Right Identity

laws001

Associativity

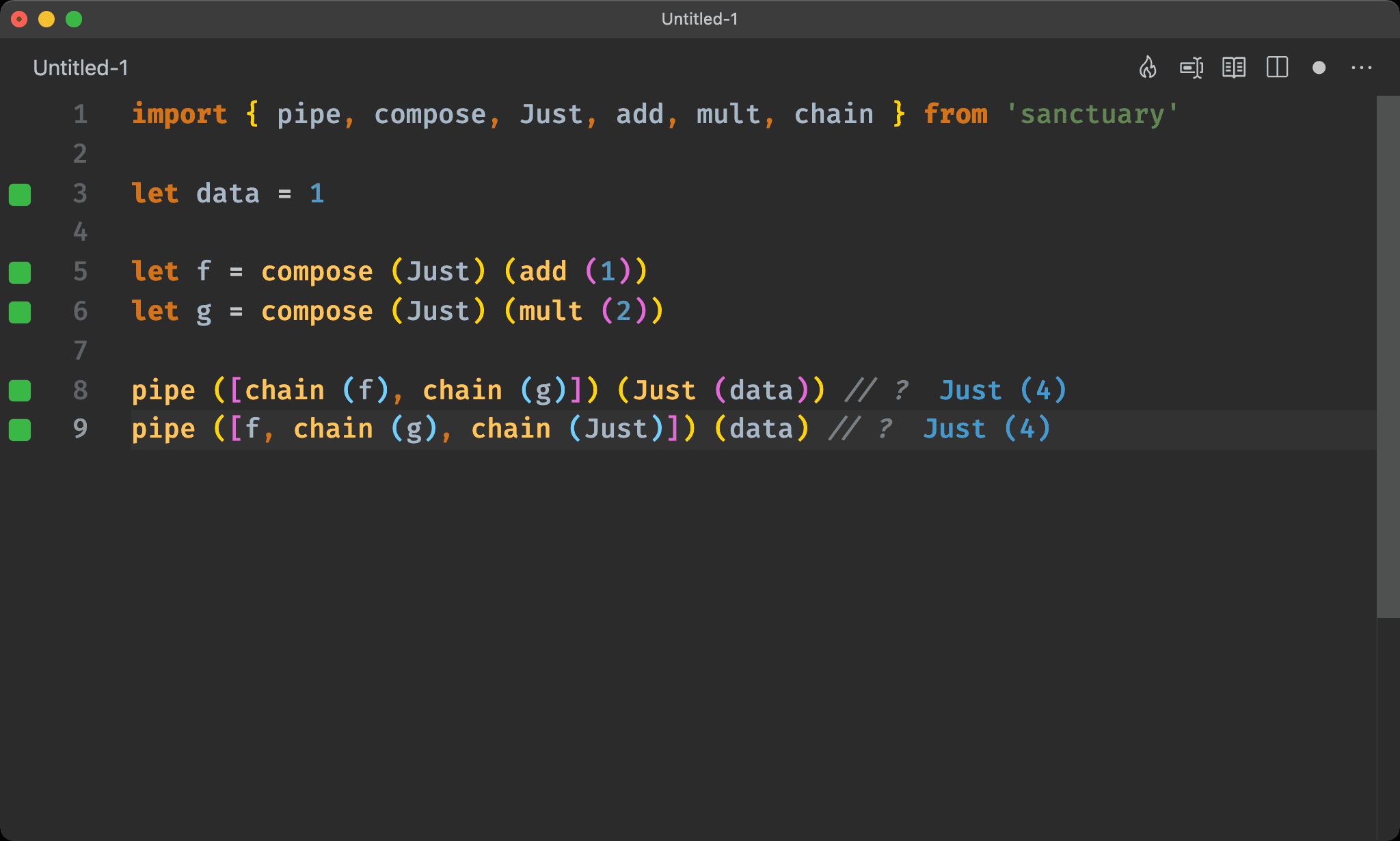
import { pipe, compose, Just, add, mult, chain } from 'sanctuary'

let data = 1

let f = compose (Just) (add (1))
let g = compose (Just) (mult (2))

pipe ([chain (f), chain (g)]) (Just (data)) // ?
pipe ([f, chain (g), chain (Just) ]) (data) // ?
  • 將 value 先包進 Monad，再連續透過 chain 使用 f 與 g 運算
  • 將 value 先經過 f 運算，再透過 chain 使用 g 運算，最後再包進 Monad

也就是先將 value 包進 Monad 再連續使用 chain 與 function 綁定，與 value 先經過 function 運算最後包進 Monad 結果相同。

Associativity
(m >>= f) >>= g === m >>= (\x -> f x >>= g)

  • (m >>= f) >>= g：使用 >>= 將 Monad 先與 f 綁定，結果再使用 >>= 與 g 綁定
  • m >>= (\x -> f x >>= g)：value 先經過 f 運算，再使用 >>= 將 Monad 與 g 綁定，最後再使用 >>= 將 Monad 與 return 綁定
  • ===：兩者結果相同

laws002

Conclusion

  • 可發現 Haskell 的 >>= infix 表示法特別適合描述 Monad Laws
  • return 在 Haskell 用來將 value 建立 Monad；在 Fandasy Land 則稱為 of，為 Applicative 必備 function，如 of (Maybe) 或 Just
  • >>= 在 Haskell 稱為 bind，在 Fantasy Land 稱為 chain，為 Chain 必備 function
  • Monad laws 包含兩個 identity law 與一個 associativity law，但並沒有 composition law，也因此 chain 只能使用 associativity law 組合 function，而無法如 Functor 那樣使用 composition law 組合 function

Reference

miklos.blog, Monad Laws for Regular Developers

# Category